10 April 2025
Prelude: Condorcet Voting
It all started when some of my friends wanted to organize a hangout. Some of us have known each other for close to 20 years, and as we’ve grown older its been harder to find time to spend with one another, so when we do, we try to make it count.
That’s why, when trying to decide on a fun activity, there’s a little bit of pressure to make sure it’s something we’re all on board with. This had an easy fix though. I just made an online form for everyone to rank the activities they wanted to do from a list we all came up with together.
The ballot my friends filled out. iSaute is a trampoline park in Montreal.
I then plugged the results of the poll into condorcet.vote which uses Condorcet methods to find the activity we are all most likely to enjoy. Condorcet methods are methods which elect candidates which are preferred to all others in a head-to-head competition. That means that if “VR Room” wins, the majority of people prefer it to all other options.
Indeed, that’s exactly what happened.
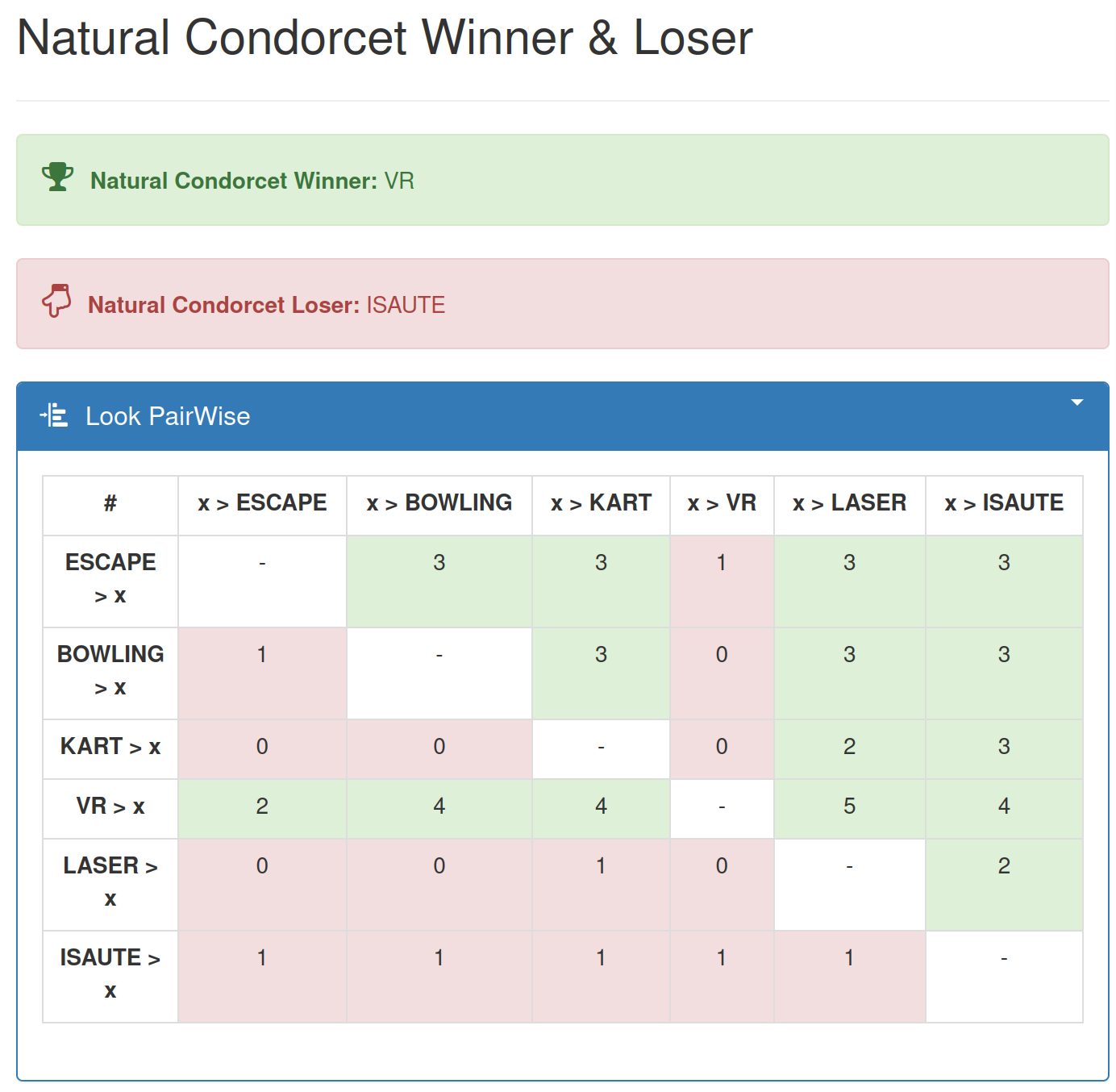
The results of the activity poll.
A Storm on the Horizon
I was still riding the high of forcing getting my friends to participate in this excercise in superior, more representative voting systems, when I was hit with some pretty bad turbulence.

This is not great. We’re sorta committed to VR, but having to split our group of eight into two groups of four felt kinda lame.
That’s until my friend George had an idea

I knew imediately what I should do

Optimizing Happiness: The Dumb Way
It’s usually not a bad idea to start with the dumbest approach you could come up with, which in this case is to brute-force the problem. Here’s how to do that:
Ranking Friendship
First, we’ll have each person rank their preferences of all other potential team mates, much as we did for the activities earlier. Let’s use the characters of acclaimed TV series Severance as a hypothetical example, with rankings I’ve come up with off the top of my dome.
| Mark | Helly | Dillon | Irving | Burt | Casey | Milchik | Cobel | |
|---|---|---|---|---|---|---|---|---|
| Mark | — | 10 | 7 | 7 | 5 | 3 | 0 | 0 |
| Helly | 10 | — | 5 | 7 | 5 | 3 | 0 | 0 |
| Dillon | 7 | 5 | — | 10 | 0 | 3 | 0 | 0 |
| Irving | 7 | 7 | 8 | — | 10 | 3 | 0 | 0 |
| Burt | 5 | 5 | 5 | 10 | — | 3 | 0 | 0 |
| Casey | 7 | 5 | 5 | 5 | 5 | — | 3 | 0 |
| Milchik | 2 | 0 | 0 | 3 | 0 | 3 | — | 0 |
| Cobel | 1 | 1 | 1 | 1 | 1 | 3 | 5 | — |
In the above table, the person in the first column has assigned scores to the person in each column, where 10 means they desire to be teamed up with this person the most, and 0 means they desire to be teamed up with this person the least.
The Sadness Function
Now that we know everyone’s preferences, we can now make a “Sadness Function” which will tell us how sad people are, having been assigned to a certain team.
The function I’ve come up with is
$$ \dfrac{1}{n^2} \sum_i^n \sum_{j, j\neq i}^n 10 - p_{i,j} $$
where \(n\) is the total number of people in a team (here \(n=4\)), and \(p\) is the preference of the \(i^\textrm{th}\) member for the \(j^\textrm{th}\) member of the team. This function will give us a “Sadness” score for a given team.
This is how I wrote this in Python
def sadness(team, p):
score = 0
n = len(team)
for i in np.arange(n):
for j in np.arange(n):
if i == j:
continue
score += p[i][j]
return score/(n**2)
So now, given the same rankings we had earlier
p = np.array([
[None, 10, 7, 7, 5, 3, 0, 0 ],
[10, None, 5, 7, 5, 3, 0, 0 ],
[7, 5, None, 10, 0, 3, 0, 0 ],
[7, 7, 8, None, 10, 3, 0, 0 ],
[5, 5, 5, 10, None, 3, 0, 0 ],
[7, 5, 5, 5, 5, None, 3, 0 ],
[2, 0, 0, 3, 0, 3, None, 0 ],
[1, 1, 1, 1, 1, 3, 5, None]
])
Exhausting Exhaustive Search
Next, we just need to measure the sadness of all possible pairs of teams:
sad_scores = []
teams = []
for team1 in combinations(np.arange(8), 4):
team2 = tuple(set(np.arange(8)) - set(team1))
team1 = tuple(team1)
# Skip equivalent configurations
if (team2, team1) in teams:
continue
sad_score = sadness(team1, p) + sadness(team2, p)
sad_scores.append(sad_score)
teams.append((team1, team2))
That leaves us with the following distribution of sadness… a “sadscape” if you will:
The distribution of sadness scores over all 35 possible team configurations.
The happiest team configuration is:
| Team 1 | Team 2 |
|---|---|
| Mark | Burt |
| Helly | Casey |
| Dillon | Milchek |
| Irving | Cobel |
The saddest team configuration is:
| Team 1 | Team 2 |
|---|---|
| Mark | Helly |
| Irving | Dillon |
| Casey | Burt |
| Cobel | Milchek |
shudder, seperating Mark and Helly, truly a sad pairing.
Genetic Algorithms: The Marginally Less Dumb Way
Exauhstive searches are great, but not all problems have 35 possible solutions like ours. Say I was charged with sorting 500 students into 50 teams of 10 for a group project. That means I’d have \(9.88 \times 10^{20}\) possible solutions to evaluate✪I’m pretty sure this is right, but it was back-of-the-napkin. Let me know if I was wrong in the comments.. Things only get hairier from there thanks to combinatorial explosion.
The next step up in complexity from an exauhstive search is using a genetic algorithm.
The Set-Up
Let’s generate some random preferences for our 500 students
p2 = np.random.randint(0,10, size=(500,500))
np.fill_diagonal(p2, 0)
To make things a little more complicated, we’ll make one of our candidates universally liked and another universally hated. This’ll make the optimization (very slightly) more interesting.
This is as easy as
p2[:,0] = 0
p2[:,1] = 10
Throwing Spaghetti at the Wall
The first step in building our model is to randomly sort people into groups.
def random_teams(num_teams, candidates):
if candidates % num_teams != 0:
raise ValueError("candidates must be evenly divisible by num_teams")
assignment = np.arange(candidates)
np.random.shuffle(assignment)
teams = np.array_split(assignment, num_teams)
return np.array(teams)
draw = random_teams(50, 500)
draw.shape
# (50, 10)
We can now measure the average sadness of the teams we generated:
def average_sadness(teams, p):
return np.average([sadness(team, p) for team in teams])
average_sadness(draw, p2)
# 4.9092
As is often the case, the next step is to throw much, much more spaghetti at the wall. Which is to say we’ll generate 100 more random pairs.
population = []
for _ in range(100):
draw = random_teams(50, 500)
population.append(draw)
The distribution of sadness scores over 100 randomly assigned teams.
Iterating on Success
We’ve only sampled \(2.014\times10^{-17}\)% of the entire space, so our odds of having landed on the best team configuration is presumably exceptionally low, especially if there is only one uniquely best option. But, we’ve certainly identified some solutions that are better than others. Let’s iterate on that success.
First, we’ll keep the top 10% best sets of team configurations.
Secondly, we’ll randomly swap teams between the top 40% sets of team configurations. This is because, among the top scorers, there are probably some happy teams lurking among the miserable. Let’s see if we can land on a winning combo by randomly swapping teams.
from random import random
population_sadness = [average_sadness(teams, p2) for teams in population]
top40 = np.array(population)[np.argsort(population_sadness)[:40]]
def cross_teams(teams1, teams2, shuffle_prob = 0.5):
for idx,(team1, team2) in enumerate(zip(teams1, teams2)):
if random() < shuffle_prob:
if random() > 0.5:
teams1[idx] = team2
else:
teams2[idx] = team1
return teams1, teams2
new_population = []
for teams1, teams2 in np.array_split(top40, 20):
teams1, teams2 = cross_teams(teams1, teams2)
new_population.append(teams1)
new_population.append(teams2)
This causes a small problem though. We now likely have some students assigned to more than one group, and some students that aren’t assigned to any, which won’t do at all. Let’s write a function that’ll replace repeated student IDs with missing ones.
from random import shuffle
def recombobulate(teams):
missing_ids = list(set(np.arange(500)) - set(teams.flatten()))
shuffle(missing_ids)
seen_ids = set()
fixed_teams = []
for team in teams:
fixed_team = []
for student_id in team:
if student_id in seen_ids:
missing_id = missing_ids.pop()
fixed_team.append(missing_id)
else:
fixed_team.append(student_id)
seen_ids.add(student_id)
fixed_teams.append(fixed_team)
return fixed_teams
While teams are now swapped between the top 40 team configurations, there’s still not a whole lot of innovation — we’re just shuffling teams in their entirety. To really shake things up, we’re going to create “mutant” teams. Here, that just means randomly swapping half the team mates from one team with another team with some random frequency. Here’s the code to do that:
def mutate(teams, mutate_prob = 0.5):
np.random.shuffle(teams)
new_teams = []
for team1, team2 in np.array_split(teams, len(teams)//2):
if len(team1) != len(team2):
raise ValueError(f"Teams must be all the same length. Found mismatched lengths {len(team1)} and {len(team2)}.")
if random() < mutate_prob:
np.random.shuffle(team1)
np.random.shuffle(team2)
half1 = team1[len(team1)//2:].copy()
half2 = team2[len(team1)//2:].copy()
team1[len(team1)//2:] = half2
team2[len(team1)//2:] = half1
new_teams.append(team1)
new_teams.append(team2)
return new_teams
Finally, we’ll make up the last 50 teams randomly to add some fresh blood into the population.
Now we can put together our procedure for iterating on our last population (which, in Genetic Algorithm parlance is termed “evolving”).
def evolve(last_generation):
last_generation = np.array(last_generation)
generation_sadness = [average_sadness(teams, p2) for teams in last_generation]
top10 = last_generation[np.argsort(generation_sadness)[:10]]
top40 = last_generation[np.argsort(generation_sadness)[:40]]
next_generation = []
# 1. Keep the top 10
for teams in top10:
next_generation.append(teams)
# 2. Randomly swap teams between and mutate the top 40
for teams1, teams2 in np.array_split(top40, 20):
teams1, teams2 = cross_teams(teams1, teams2)
# ensure that students aren't assigned to multiple teams
# or that students are missing
teams1, teams2 = recombobulate(teams1), recombobulate(teams2)
teams1, teams2 = mutate(teams1), mutate(teams2)
next_generation.append(teams1)
next_generation.append(teams2)
# 3. Add 50 new fresh teams
for _ in range(50):
teams = random_teams(50, 500)
next_generation.append(teams)
return np.array(next_generation)
Great! We’ve now code that would bring a tear to Darwin’s eye✪Pay no mind as to whether it’s a tear of joy or sorrow.. Now, all we have to do is iterate through multiple generations. How many generations is a tough question to answer, but the answer lies somewhere between “until Sadness stops decreasing” and “for as long as you have time”. I’ve already spent too much time on this, so I’ll run it for about 10 minutes worth of generations, which happens to work out to 1,000 generations. Here’s the code I came up with to run genetic algorithm. Note, I’m also drawing a random sample each generation, just to see how dumb luck compares to our genetic algorithm.
# Create the zeroth generation
# This is just a random sample
gen_zero = np.array([random_teams(50, 500) for _ in range(150)])
next_gen = gen_zero
# Where we store the sadness scores for our genetic algorithm
# after every epoch
best_genetic_sads = []
# ...and for our random samples
best_random_sads = []
for i in range(1000):
# A new generation from our Genetic Algorithm
genetic_sads = [average_sadness(teams, p2) for teams in next_gen]
next_gen = evolve(next_gen)
# A new random sample for our baseline
random_gen = np.array([random_teams(50, 500) for _ in range(150)])
random_sads = [average_sadness(teams, p2) for teams in random_gen]
# Log it
best_genetic_sads.append(min(genetic_sads))
best_random_sads.append(min(random_sads))
And after a thrilling 10 minutes of watching paint dry to the tune of my laptop fans running at top speed, it looks like our Genetic Algorithm has reduced our sadness!
Now, if I’m totally honest, I don’t know how much sadder 4.85 is compared to 4.7, and whether that’s to be celebrated on its own. I can, however, check to see how much of an improvement this is over our random sampling:
Well, that looks like a stark difference. By chance, we landed on a team configuration of just shy of 4.8, which is indeed more sadness than the ~4.7 the genetic algorithm scored. What’s more, with as many possible combinations as there are in this problem space, it’s very likely the genetic algorithm could score a lot better if you gave it, say, twice as long.
Prologue
Wait, what teams did you end up sorting into?
Ok, so the jig is up. Genetic algorithms did not end my longest friendships, nor has an exauhstive search. We are normal(-ish) people who, rather than rank their friends who they all like well enough and run a computer simulation of their sadness in all possible scenarios, decided to just pick a team in the order we showed up to the VR place. This did mean that romantic partners in the group ended up together, which probably decreased sadness a bit.
How do I end my long-standing friendships with GAs? I came here for answers, damn it!
Just start talking to your friends about genetic algorithms. It always seems to get them to leave in a hurry for me.
“Please try to enjoy each team equally…”
So, I was curious whether it might be desireable to reduce the disparity of sadness between groups, whether than minimizing overall sadness. This means that we can find solutions where, even though one of the teams is not as happy as it possibly could be, the other team might be slightly happier, thereby more evenly spreading the misery as a bit of a compromise.
To do this, I came up with a new “isosadness” score given as
$$ S_\textrm{iso} = \frac{1}{2} \times (S_1 + S_2) \times \frac{S_1}{S_2} $$
where \(S_\textrm{iso}\) is the isosadness, \(S_1\) and \(S_2\) are the sadness of both teams, where \(S_1 > S_2\). This is just the product between the ratio of the two sadnesses and their average. You can simplify the expression as
$$ S_\textrm{iso} = \frac{S_1(S_1 + S_2)}{2S_2}. $$
This is a visualization of the isosadness of all 35 possible teams in the Severance example:
Isosadness is indicated by the colour of the markers.
This results in the following grouping having the lowest isosadness:
| Team 1 | Team 2 |
|---|---|
| Mark | Dillon |
| Helly | Irving |
| Casey | Burt |
| Milchek | Cobel |
Notably, Mark and Helly, and Dillon and Irving are still paired up, but Cobel and Milchek are split up. Also, Burt & Irving are also together at last. I’ll be honest, I think these pairing make far more sense than the original greedy approach.