Deciphering interaction fingerprints from protein molecular surfaces using geometric deep learning

Authors: P. Gainza et al.

DOI: 10.1038/s41592-019-0666-6

Wherein the authors propose MaSIF, a "conceptual framework" for creating feature embeddings of protein structures which are suitable for predicting protein interactions. They apply a CNN to radial patches in geodesic space (more on that here) to learn these embeddings. The authors show MaSIF embeddings to be an effective basis for binding-site prediciton and PPI prediction.

18 May 2020

Motivation

Predicting protein-protein interactions is extremely important to understanding how and why cells do what they do. There are a number of ways to think of protein interactions, but structural biologists like to consider the three-dimensional structure of proteins and how two proteins interface in space. Think of how you might get two strangely shaped pieces when you build IKEA furniture; you know they are meant to fit together, but understanding how (or even why) often requires the assembly instructions.

Towards Generalising Surface Features

To understand how proteins interact in 3D space, the authors note that previous researchers have created ways to annotate the surface of proteins using clever features they came-up with using expert knowledge ✪The ones mentioned in the paper are “Zernike desriptors” and geometric invariant fingerprints (GIFs).. If you’ve a background in ML, you might know first-hand that crafting good features is really hard — there always seems to be some edge case or combination of features you’ve forgotten and getting a decent signal-to-noise ratio is a challenge. One of the big selling points of deep learning is that it eliminates the need for feature engineering, as the hidden layers are like little feature engineers themselves, each layer composing features from the last to create new features in such a way that optimises the loss function.

The authors of this paper supply their model with information about the 3D space of the protein, as well as some chemical properties of the amino acids that make up the proteins. The model then integrates all that information to create a final feature vector that is used for some ultimate task (e.g.: predicting protein interactions).

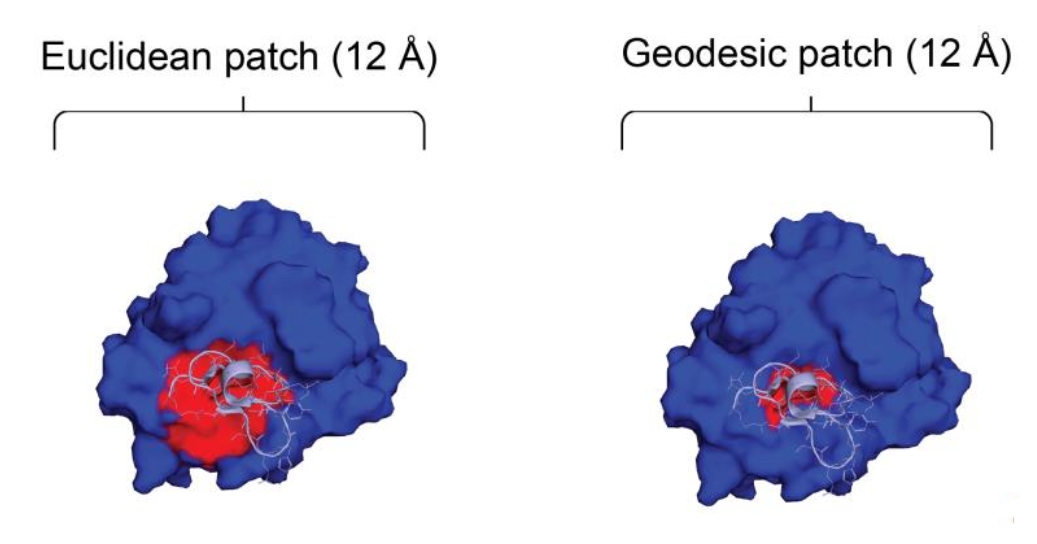
Geodesic vs. Euclidean Geometric Learning

Another neat thing about this method is the use of geodesic distances instead of euclidean distances. The model considers seperate radial patches (think of circles drawn on the surface of the protein) at a time. The radius of these patches is some fixed distance, but the authors claim that how you measure that distance makes all the difference.

If you use Euclidean distances, you would simply draw a circle where the radius is any straight line of length \(r\) from the the centre point of the patch. In Geodesic space, instead of drawing a straight line from the centre, you can imagine rolling a ball or being shrunk down and walking some distance \(r\) from the centre. Because proteins can have very irregular shapes and deep pockets, Euclidean surface distances are often the wrong choice✪The better your surface is approximated by a sphere, the better Euclidean distances are for this type of problem. Proteins are very much not spheres as much as e.g. biophysics likes to pretend. (See Figure 2).